Chapter 10 Conclusion&Outlook
greeNsort® has rewound sorting research back to 1961 where Toni Hoare invented Quicksort and even further back to 1945 when John von Neumann described Mergesort. From there greeNsort® went on a journey through binary sorting in contiguous space. greeNsort® identified and challenged common core-beliefs of the prior art associated with these algorithms, introduced a web of innovations and suggested a classification for them.
greeNsort® introduced a method for measuring sustainability of algorithms that considers not only RUNtime Energy but also hardware %RAM requirements and combines both into the Footprint measure which allows a fair comparison of algorithms with different memory requirements.
greeNsort® introduced the Ordinal-machine model that motivates robust algorithms which reduce access- and move-distances. Distance-reduction is an under-appreciated feature of Quicksort, and after resolving the Quicksort-Dilemma much of the greeNsort® project is about bringing distance-reduction to Mergesort and other Divide&Conquer algorithms which in the prior art move elements between two distant memory regions.
greeNsort® then introduced Symmetric-asymmetry, an important principle in many sciences, which surprisingly misses in computers science. Sorting and the von-Neumann machine is rife with asymmetries, namely Access-asymmetry, Buffer-asymmetry, Order-asymmetry, Pivot-asymmetry and Tie-asymmetry. Introducing symmetry into problem-solving with these asymmetries results in an enhanced solution space that contains many new methods and algorithms.
Donald Knuth’s mathematical definition of sorting into Ascending (Asc) and Descending (Desc) addressed Order-asymmetry but ignored Access-asymmetry which arises as soon as sorting is done in a one-dimensional virtual memory that has left to right positions. greeNsort® introduces a new definition of Symmetric-sorting which differentiates ascending into Ascending from Left (AscLeft) and Ascending from Right (AscRight). Using the example of Bimesort it was explained that unstable algorithms can be the consequence of confusing right-ascending with left-descending.
greeNsort® explained that many asymmetric problems can be resolved with Symmetric-recursion, for example the Quicksort-Dilemma – a result of Access-asymmetry and Pivot-asymmetry. Replacing two persistent prior art beliefs by No3rd partition and Asymmetric-partitioning, the solutions were elegant: combining the (symmetric) B-level innovation – (F)ast (L)oops (I)n (P)artitioning (FLIP) and the (lean) B-level innovation – (D)istinct (I)dentification for (E)arly (T)ermination (DIET) methods enabled with the Z:cksorts exactly those symmetric probabilistic algorithms that Tony Hoare tried to design with Quicksort1. Replacing the DIET with the B-level innovation – (P)re-(O)rder (E)arly (T)ermination (POET) method resulted in the even more adaptive Ducksort. This use of symmetry seamlessly led to partial sorting algorithms which consistently handle ties and return more useful information.
greeNsort® explained the space-time trade-off in Mergesorts and the Mergesort-dilemma: that the prior art knows either efficient Knuthsort needing 100% buffer or adaptive but inefficient like Timsort needing 50% buffer. greeNsort® explained that unlike Bimesort, Knuthsort can be made \(\mathcal{O}(N)\) adaptive like Timsort. Introducing Data-driven-location enables Omitsort and combining this with core-belief Undirected-sorting and a new method Data-driven-order enables the bi-adaptive Octosort.
Then with a detour over new methods and algorithms (Gapped-setup, Gapped-merging, GKnuthsort, Buffer-merging, TKnuthsort, Crocosort) greeNsort® arrived at Symmetric-merging which allows distance reducing merging with only 50% buffer or less. Two basic algorithmic methods with different adaptivity were introduced (Frogsort, Geckosort) and several implementation variants explained (Frogsort0 and Frogsort1 with 50% buffer, Frogsort2 with 14% buffer and even much faster than the competition. Alternative to Buffer-merging in the Split&Merge paradigm, greeNsort® suggested Buffer-sharing in the Share&Merge paradigm, which enables Frogsort3 with even lower memory requirements (12.5% by default). The Frogsorts 1,2,3 can be joined in doubly parametrized Frogsort6.
greeNsort® then combined Symmetric-merging with the Data-driven-order method of Omitsort to obtain the bi-adaptive Squidsort algorithms, implemented Squidsort1 and Squidsort2 to show that they provide significant \(\mathcal{O}(N \cdot \log{N})\) adaptivity while – unlike Timsort, Peeksort and Powersort – keeping nocopy-efficiency in hard sorting tasks.
greeNsort® investigated some – possibly new – methods for merge-sorting with \(\sqrt{N}\) buffer or less and found that \(\sqrt{N}\) algorithms (particularly Walksort, Jumpsort) have better Footprint than prior art \(N\log{N}\) algorithms, but not better than the simpler and more general Frogsort2 with 14% buffer.
greeNsort® then turned to an under-appreciated generality of Mergesorts: that they can directly sort elements of varying size. Under the C-level innovation – (D)irect (S)orting (D)ifferent (S)ize (DSDS) paradigm, two methods B-level innovation – (D)irect (S)orting (N)ull-terminated (S)trings (DSNS) and B-level innovation – (D)irect (S)orting (P)ointered (E)lements (DSPE) where presented, and the former used to implement VKnuthsort (100% buffer ) and VFrogsort1 (50% buffer) which use less Energy (and the latter less memory) than direct sorting methods such as UKnuthsort, WQuicksort2 or UZacksort.
greeNsort® completed its exploration of new algorithms by diving into the Partition&Pool paradigm, where – as an exception – Wing-partitioning allows stable binary-partitioning with a single pass over the data per recursion level. greeNsort® implemented Kiwisort (using 100% distant buffer), introduced Buffer-partitioning and particularly Symmetric-partitioning with Gapped-wrapup to obtain Swansort (using 100% local buffer) and finally the travelling Storksort (using 50% local buffer) which can serve an exotic use-case (sorting over a wire).
greeNsort® compared a couple of parallel implementations to substantiate the claim that Symmetric-merging is as general as prior art merging. greeNsort® explained its preferred method for lean parallel merging (lean-parallel-merging) and how to parallelize Symmetric-merging (parallel-Symmetric-merging). After applying them to some of the above algorithms, it was shown that PFrogsort0, PFrogsort1, PFrogsort2 and PFrogsort3 parallelize almost as well as PKnuthsort.
greeNsort® finally glimpsed on the impact on Incremental sorting, priority-queues and sorted dictionaries. Using the greeNsort® classification, the height of the innovations can be quantified: Paradigmatic changes comprise of 12 new core beliefs (C-level innovations) and a new definition of sorting itself (D-level innovation). greeNsort® has introduced 20 new methods (B-level innovations) and 12 further methods (probably known T-level techniques) that allowed to design new algorithms. Here I reported 21 new algorithms, 9 extended algorithms and 8 further algorithms (A-, E- and F-level innovations).
Finally we looked on the Impact of greeNsort® on computational Thinking, Research, Teaching, Libraries, APIs, IDEs, Languages, Compilers and Hardware. Most important: the hand-coded Symmetric-recursion in the test-bed can also be generated with formal Code-mirroring, which leads to Symmetric-languages, mirroring Symmetric-compilers and supporting Symmetric-hardware instructions.
In summary: the aesthetic and ethical compass of the greeNsort® journey lead to simplicity and sustainability, also robustness and resilience. The focus was on design – for low distance. The contribution to research is the revision of sorting and bringing symmetry to computer science. The contribution to teaching is its beauty of concepts and its poetry of code. Welcome to the new era of symmetric sustainable sorting with better trade-offs between generality, simplicity, adaptivity and efficiency. Welcome also to a new field of research: investigating the implications of Symmetric-asymmetry, Symmetric-recursion and Code-mirroring on programming languages, compilers and hardware.
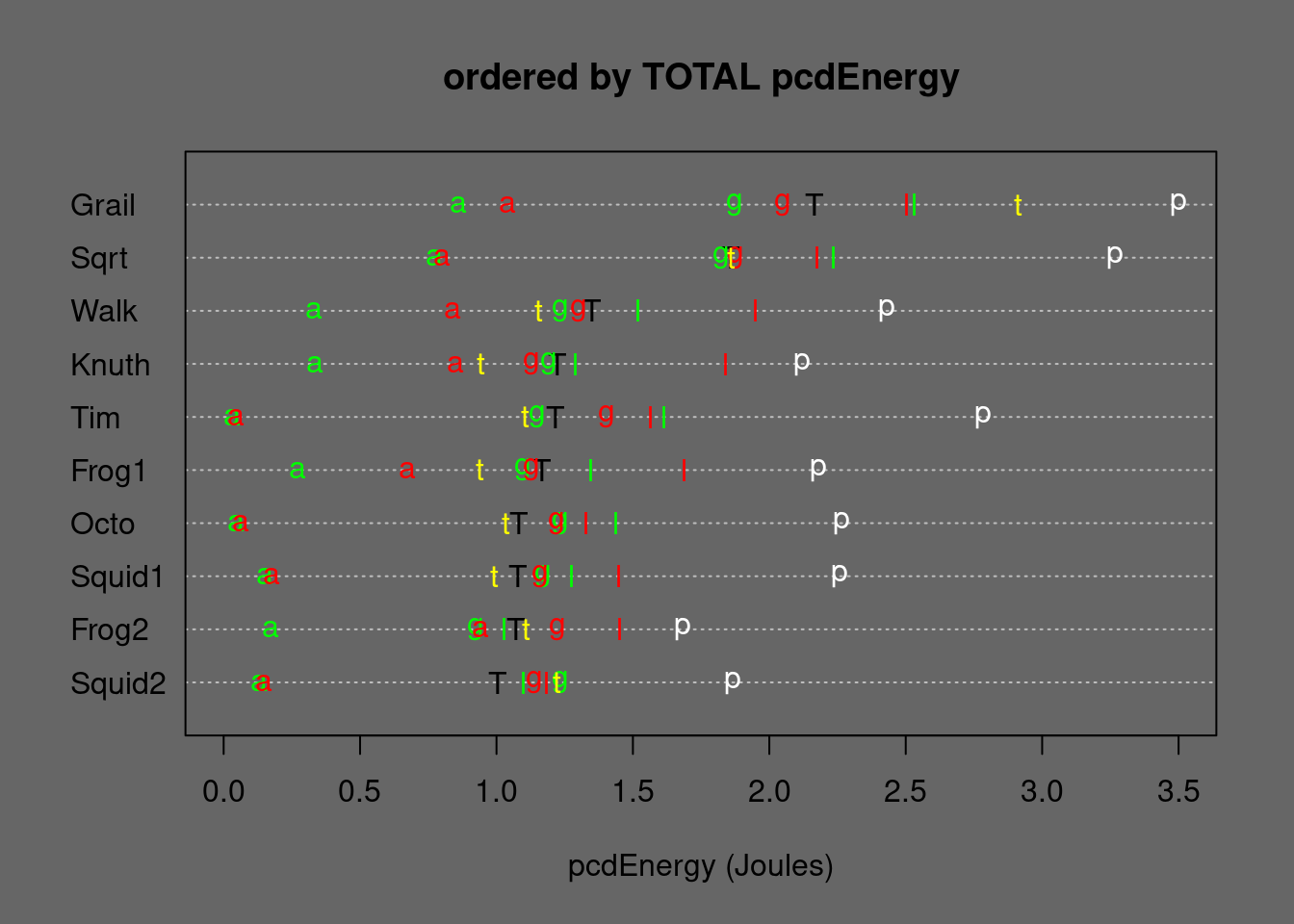
Figure 10.1: Medians of important algorithms ordered by TOTAL Energy. T=TOTAL, p=permut, t=tielog2; green: a=ascall, g=ascglobal, l=asclocal; red: a=descall, g=descglobal, l=desclocal
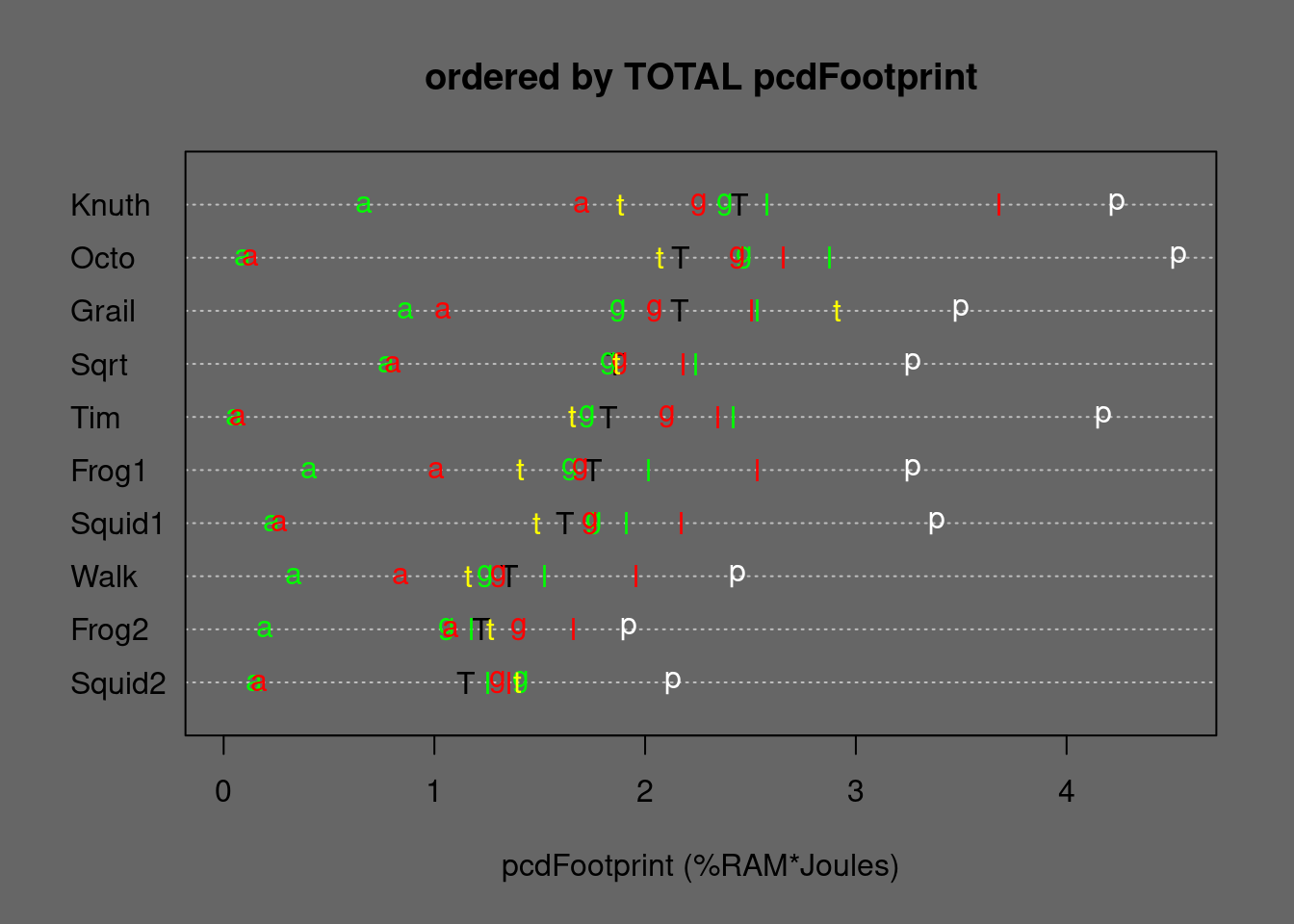
Figure 10.2: Medians of important algorithms ordered by TOTAL eFootprint. T=TOTAL, p=permut, t=tielog2; green: a=ascall, g=ascglobal, l=asclocal; red: a=descall, g=descglobal, l=desclocal