Chapter 2 Paradigmatic innovations
2.1 Ordinal-machine model
innovation("Ordinal-machine","C*","minimize monotonic cost of distance")The prior art uses specific machine models, like the random-access-model or the IO-model with specific assumptions on the costs for accessing and moving data. Those machine models are the basis for analyzing algorithms and proving certain properties. This precise mathematical approach suggests that those machine models represent real machines, which is rarely the case. Furthermore this approach focuses academic efforts on analysis and proof rather than on development of better algorithms. Algorithms and even software have a longer lifetime than particular machines, therefore they should be robust against variations in technology and resilient in environment with little hardware resources. The algorithm developer cannot know on which machines his code will run, more and more he cannot even know the details of current machines, because they are more and more virtualized in the cloud. Hence greeNsort® follows a different approach. A non-specific Ordinal-machine model simply assumes that the cost of access and moves is a monotonic function of distance in a memory address space that reaches from left to right. For a constant distance cost in the classic random-access-model there is a constant \(\mathcal{O}(1)\) cost per move, linear \(\mathcal{O}(N)\) cost per level and \(\mathcal{O}(N\log{N})\) for the total cost of Divide&Conquer sorting. Now consider the popular AlgoRythmics videos which teach sorting by folk-dances: the movement cost of the dancers on stage is a linear function of distance, hence the cost of the same sorting algorithm is suddenly \(\mathcal{O}(N)\) per move, quadratic \(\mathcal{O}(N^2)\) cost per level and \(\mathcal{O}(N^2\log{N})\) for the total cost of Divide&Conquer sorting. Today’s computers have distance costs in between, say \(\mathcal{O}(\log{N})\) per move, \(\mathcal{O}(N\log{N})\) per level and \(\mathcal{O}(N\log{N}^2)\) for the total cost of Divide&Conquer sorting.
From a practical point of view, assuming a Ordinal-machine focuses on quick iteration of developing new algorithms, experimenting with them and improving them, rather than proving mathematical properties based on pseudo-exact machine-assumptions. For greeNsort® this implies a focus on distance minimization and sustainable measurement.
2.2 Sustainable measurement
innovation("Footprint","C*","measure variableCost x %fixedCost")The prior art empirically evaluates algorithms by measuring RUNtime, CPUtime or by counting certain operations such as, comparisons, moves, swaps, cache-misses etc. This addresses the CO2 variable cost of running the software but ignores the CO2 fixed cost embodied in producing the hardware4. greeNsort® introduces the Footprint, which multiplies variable cost with relative fixed-cost (per element, not absolute). greeNsort® uses:
- (R)andom (A)ccess (M)emory (RAM) as a proxy and %RAM as a normalized proxy for fixed cost hardware requirements,
- Energy (RAPL), or simpler CPUtime or RUNtime as proxies for variable costs of running the software
- tFootprint, cFootprint and eFootprint as single-scale measures of variable costs penalized for fixed costs (runTime, CPUtime and Energy multiplied with %RAM)
Footprints allow to compare algorithms with different memory-speed trade-offs. Optimizing for Footprints avoids the pitfalls of extreme choices: just minimizing CPUtime or Energy can lead to excessive memory (and hardware) consumption; attempting in-place sorting with zero-buffer-memory has been of great academic interest but never lead to practically convincing algorithms. This new paradigmatic choice of measuring algorithms has enabled greeNsort® algorithms with better memory-speed trade-offs aka better trade-offs between execution CO2 of electricity and embodied CO2 of hardware. For details on measuring RAPL-energy and eFootprints see the Methods&Measurement section.
2.3 Symmetry principle
innovation("Symmetric-asymmetry","C*","low-level-asymmetry, high-level-symmetry")2.3.1 Symmetry
In biology, engineering and architecture symmetry plays an important role, particularly bi-symmetry. But strangely not in Computer Science! Yes, there are publications on symmetry detection algorithms, but there symmetry is only the object, not the subject of the design: Symmetry is rarely considered a major design principle for algorithms and code. Although a one-dimensional left-right-memory-address-space should be an invitation for bi-symmetry.
A notable exception is Quicksort1, which was designed symmetrically by Hoare (1961b), Hoare (1961a): two pointers move from left and right until they meet an element that is on the wrong side. Unfortunately the search cannot be symmetric in a von-Neumann-Machine: first one pointer searches, then the other, this can create heavy imbalance, hence can lead to \(\mathcal{O}(N)\) recursion depth and \(\mathcal{O}(N^2)\) execution cost for certain inputs. The popular Quicksort2 which goes back to Singleton (1969) stops pointers on pivot-ties: this guarantees a balanced partition but at a costly price: pivot-ties are swapped with no benefit and worse the partitioning is not MECE and does not early-terminate on ties.
Symmetric pointer search can be approximated by alternating between moving the left and right pointer. The greeNsort® algorithm Chicksort implements this, and it indeed avoids swapping pivot-ties, but it is slower than Quicksort2 due to the more complex loop structure. I did not explore block-wise alternating pointer search, because there is a much better solution (see the The Quicksort-Dilemma).
In biology, engineering and architecture symmetry is often composed high-level from low-level asymmetries. greeNsort® is built on transferring the Symmetric-asymmetry concept to computer science: C-level innovation – embracing low-level-asymmetry within high-level-symmetry, see Symmetry principle
2.3.2 Asymmetries
The von-Neumann-Machine is rife with asymmetries
- Access-asymmetry the fact that memory access is asymmetric either the left element first then the right one or the right element first and then the left one, see Asymmetries
- Buffer-asymmetry the fact that buffer placement relative to data is asymmetric, data may either be placed left of buffer memory (DB) or right of buffer memory (BD), see Asymmetries
as is the topic of sorting
- Order-asymmetry the fact that that ‘order’ is asymmetric and reaches from ‘low’ to ‘high’ ‘keys’, see Asymmetries
- Pivot-asymmetry the fact that a binary pivot-comparison (one of [LT], [LE], [GT], [GE]) assigns an element equal to the pivot either to one partition or the other, see Asymmetries
- Tie-asymmetry the fact that stable ties are asymmetric, they may represent their original order either from left to right (LR) or from right to left (RL), see Asymmetries
How does one embrace low-level-asymmetry within high-level-symmetry? Let’s start with a new definition of sorting.
2.4 Definition of sorting
innovation("Symmetric-sorting","D","'ascleft', 'ascright', 'descleft', 'descright'")According to Knuth D. E. Knuth (1998), p. 1 sorting is “the rearrangement of items into ascending or descending order” and can be distinguished into stable and unstable sorting. This definition creates four different goals for sorting “unstable ascending”, “unstable descending”, “stable ascending”, and “stable descending”. Sorting libraries implement all four or a subset of these four. From Knuth’s mathematical perspective the definition of sorting is perfect.
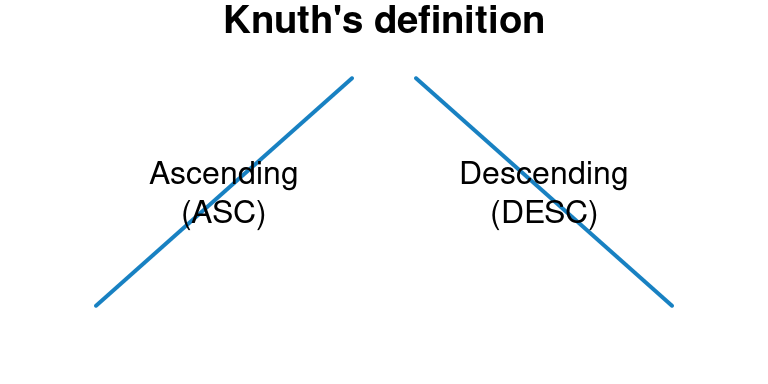
Figure 2.1: Knuth’s definition of sorting
However, in the context of computers, algorithms are not abstract, they operate on elements that are stored in memory that is addressed from left to to right address locations (address locations are notated here from left to right in order to not confuse this with low and high sorting keys). Habitually ascending and descending sequences are written from left to right :
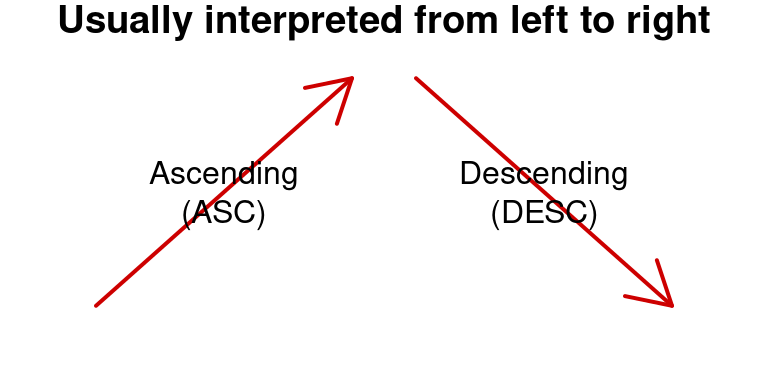
Figure 2.2: Conventional interpretation: from left to right
The two abstract sorting sequences Ascending (Asc) and Descending (Desc) correspond to four concrete sorting sequences in memory: Ascending from Left (AscLeft), Ascending from Right (AscRight), and Descending from Left (DescLeft), and DescLeft. The Difference between DescLeft and AscLeft, is a reverted - but stable - sequence of ties!
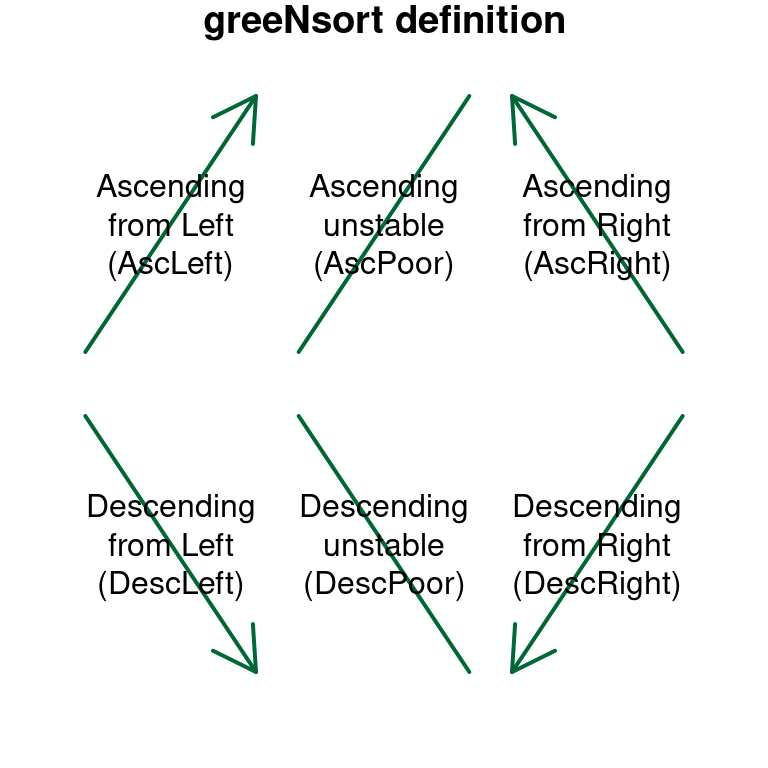
Figure 2.3: greeNsort definition: unstable sorting has two API targets (AscPoor, DescPoor) but stable symmetric sorting has four API targets (AscLeft, AscRight, DescLeft and DescRight)
A first example for the immediate benefits of the greeNsort® definition is found in section Reference algo (Knuthsort). The greeNsort® definition is powerful because it facilitates reasoning and increases the size of the solution space, like the invention of the imaginary part increased the number space from real numbers to complex numbers, such that suddenly the square-root of a negative number was defined.
2.5 Recursion model
innovation("Mutual-recursion","T*","is more expressive than self-recursion")
innovation("Symmetric-recursion","C*","symmetric mutual recursion")
dependency("Symmetric-recursion", "Mutual-recursion")
dependency("Symmetric-recursion", "Symmetric-asymmetry")
dependency("Symmetric-recursion", "Code-mirroring")Some people consider recursion to be a technical topic, and tail-recursion indeed is. However, recursion is first and foremost a mental tool, that helps humans to organize code and understand algorithms. Proof? Because each recursion can be written as loops. QED.
In the context of sorting algorithms prior art recursion usually means self-recursion. However, there are good reasons – explained in the book – to assume that Mutual-recursion is a more natural and powerful mental problem-solving device than self-recursion. Even without this assumption: mutual recursion is definitely more expressive than self-recursion. Mutual-recursion is not new5, but undervalued. Why? Because mutual-recursion is a natural fit for binary Divide&Conquer algorithms.
Divide&Conquer in sorting means dividing and conquering address ranges, i.e. ranges from left to right. greeNsort® is built on Symmetric-recursion, a new class of mutual-recursions where two functions co-operate recursively in a more or less symmetric fashion, and where the symmetry axis is left-right memory, not ascending-descending order.
And here is the final answer to the question how to embrace low-level-asymmetry within high-level-symmetry: instead of the failing prior art approaches to achieve symmetry in loops, greeNsort® embraces asymmetry in loops and creates a higher-level symmetry in mutual-recursion. You will soon see this at work.
2.6 Mirroring code
innovation("Code-mirroring","C*","left-right mirroring of code")
innovation("Symmetric-language","C*","symmetric programming language")
dependency("Symmetric-language", "Code-mirroring")
innovation("Symmetric-compiler","C*","compiling symmetric language")
dependency("Symmetric-compiler", "Symmetric-language")
innovation("Symmetric-hardware","C*","instructions for mirroring code")
dependency("Symmetric-hardware", "Symmetric-compiler")The Wikipedia entry for binary search contains one of the few references to symmetric behavior: searching for the leftmost or rightmost element in case of ties. However, that the two functions given behave symmetrically is not easy to see, because the code is not symmetric. Achieving symmetry by mirroring the code itself has advantages: it is easier to verify correct and code-mirroring can be done formally and automatically.
As a research project, the greeNsort® algorithms have been developed and written largely manually. But the symmetric properties of the two functions calling mutually in Symmetric-recursion are an invitation to create one of them by mirroring code sections of the other, either with meta-programming techniques or with new language constructs that support Code-mirroring, see the demonstration of the feasibility of Code-mirroring in a (interpreted) R-implementation of Zacksort in the Languages section. If code-mirroring is supported by languages, compilers and hardware, then the cost of code-duplication in Symmetric-recursion can be avoided. The opportunity is: writing elegant parsimonious code once, mirror-it with language constructs and the compiler translates this into hardware-instructions for mirroring sections of instructions. This is a promising new field of research.
2.7 Further techniques
innovation("Divide&Conquer","T*","Recursive divide and conquer paradigm")
innovation("COMREC","T*","COMputing on the RECursion")
innovation("NORELORE","T*","NO-REgret LOop-REuse")
innovation("DONOTUBE","T*","DO NOt TUne the BEst-case")
dependency("Mutual-recursion","COMREC")In the broadest sense, mutual recursion is a special case of a broader technique: T-level technique - (COM)puting on the (REC)ursion (COMREC). COMREC is a simple powerful technique, not as complicated and expressive as meta-programming. Meta-programming tends to be not only expressive but also inefficient, particularly programming on the language in interpreted languages such as R or Python6. COMREC can be easily compiled to efficient executable code. Beyond Symmetric-recursion, further examples of this technique are nested recursive functions, where different functions are used for different problem sizes. The most popular use-case is tuning with Insertionsort for problem sizes smaller than a cut-off, the greeNsort® algorithms use an INSERTIONSORT_LIMIT of 64.
Equal tuning is an example of another greeNsort® principle: equal implementation quality for fair comparison. An exception is Timsort, which violates the simplicity-principle and hence the test-bed uses an existing implementation, see 2nd Reference (Timsort).
Finally, three principles should be mentioned, that are immediately applied in the section on Quicksort algorithms:
Robustness: greeNsort® Partition&Pool algorithms are using random pivots which guarantees a \(\mathcal{O}(N\log{N})\) average case for any data input. Using deterministic pivots cannot guarantee an \(\mathcal{O}(N\log{N})\) average case, the analyses of Sedgewick (1977b) which claim this are based on the nonsense-assumption that instead the input data be random, this is irresponsible for production use (unless recursion-depth is guarded and limited as in Introsort).
NORELORE: greeNsort® algorithms use optimizations that avoid extra-operations and memory scanning by reusing and melting loops for different purposes.
DONOTUBE: greeNsort® algorithms may invest extra-operations to enable best-case behavior but do not invest extra-operations to speed-up best-cases.
The Green Software Foundation has recently (2021) suggested the Software Carbon Intensity (SCI), which attempts an end-to-end measurement of variable costs and fixed costs on a common CO2-scale. This, however, is not pragmatic: it considers factors that are not attributes of software and that are not available to software developers (energy/instruction of hardware, CO2/energy of location). Furthermore the SCI has the paradoxical feature that in locations with 100% renewable energy the electricity is assumed to have zero costs such that purely the hardware amortization determines the SCI. For more details see my comment to the SCI and my presentation at the GSF↩︎
In sorting it is rare, I am aware only of Sedgewick’s “superoptimization” which combines nocopy-Mergesort with a bitonic merge strategy, see First algo (Bimesort)↩︎
for the inefficiency of Python see Enhancing the Software Carbon Intensity (SCI) specification of the Green Software Foundation (GSF)↩︎